Actualizado: 03 de abril de 2025
Cómo saber cuándo operar y cuándo no
Nota importante antes de empezar:
Este artículo puede darte eso que necesitas para pasar de irregular a consistente. Contiene información muy valiosa, y además trae un regalo para ti al final, pero tienes que estar preparado para leerlo con atención.
Ser bueno no basta, hay que saber elegir las operaciones
Vamos a plantearlo del modo más bruto posible. Lo que quiero es que te des cuénta del problema que hay detrás:
¿Cuál es el mejor método para saber si debes ejecutar cierta operación o dejarla pasar?
Respuesta:
Adivinar el futuro, comprobar si la operación saldrá ganadora o perdedora y ejecutarla si es que vas a ganar o dejarla pasar si es que vas a perder.
Este método nunca falla. Es perfecto. Así sabes si te compensa operar o no.
Sólo tiene un problema: No podemos adivinar el futuro (Sí, lo siento ¡Yo también me hice ilusiones al principio!).
El reto es saber si me mojo o no me mojo ¡No quiero perder dinero!
El problema de fondo es que puedes operar y dedicarte a perder. Si nunca ganas, o cuando ganas, ganas tan poco que no compensas las pérdidas de las operaciones perdedoras ¡no te compensa operar! Pero ¿cómo saberlo de antemano?
La solución
La solución pasa por aceptar un compromiso:
Acepto perder dinero de vez en cuando si en global acabo ganando.
Dicho con otras palabras: No me importa (ojo, me fastidia, pero lo asumo) perder dinero en mi próxima operación; pero tengo que saber que, cuando gane, voy a ganar más que cuando pierda; ya sea porque ganaré muchas más veces de las que perderé, o porque cuando gane, ganaré más de lo que perderé cuando pierda.
Es decir, renuncias a ganar siempre (lo que nos libra de inventar una máquina del tiempo ¡menos mal!) a cambio de saber que te compensa operar, porque en global sí que vas a ganar.
Ahora el problema es cómo saber que, en global, vas a ganar.
¿Cómo se logra esto?
Con la combinación de tres cosas a la vez:
1.- Operando siempre igual
Esto te permite apoyarte en lo que se llama inferencia estadística, que no es ni más ni menos que basarte en la hipótesis de que, si lo haces siempre igual, tendrás unos resultados similares.
Nota: Esto que suena tan tonto (operar siempre igual) en la práctica es uno de los retos más duros para un trader, especialmente para un trader novato. Realizar veinte o treinta operaciones sin variar el método se convierte en tarea imposible para no pocos.
¡Ojo al dato! Puede que lleves tiempo frustrándote porque no consigues ganar de forma consistente ¡sólo por este motivo!
2.- Haciendo la cuenta mágica
Basándote en tus resultados previos (ahora que puedes, porque responden todos a un método común) puedes echar la cuenta mágica.
Esta cuenta mágica te permite decidir en qué operación te sale rentable arriesgarte y en cuál no.
Fíjate que la cuenta mágica no adivina si ganarás o perderás, sino que te dice si esta operación es de las que, en global, te llevarán a ganar (¡incluso aunque luego salga perdedora!)
Enseguida vemos esa cuenta mágica. Ahora quiero que prestes atención sólo al concepto.
3.- Ejecutando sólo aquellas operaciones que te compensan
La realidad del trading es que nos surgen infinidad de oportunidades constantemente, pero no hay dos iguales. Por eso cuesta mucho diferenciar cuándo nos compensa entrar y cuándo no.
Con los dos pasos anteriores, lo que logramos es un esquema controlado: Sabemos que, con las operaciones de este tipo (el tipo que sea que tú operes) que cumplen con la cuenta mágica, en global, acabamos ganando.
Esto es muy potente. Salvo la máquina del tiempo, que era incluso mejor, es lo más potente y fiable que puedes tener en trading: Una guía que te lleva a ganar dinero de forma consistente.
Eso sí, si tienes una guía, respétala.
Segunda nota: De nuevo, parece que te cuento una obviedad; pero la realidad me demuestra todos los días que la mayoría de la gente es incapaz de no operar algo que parece muy bueno, pero que no entra dentro de su esquema controlado.
Un paso necesario para la cuenta mágica
Si tú ganases siempre, no tendrías nada que pensar; aunque fuera para ganar sólo un céntimo, te compensaría operar, porque sabes seguro que lo ganarás.
En cambio, si no ganas casi nunca, la cosa cambia: Tienes que asegurarte de que arriesgas poquísimo y que en cambio, de ganar, ganarás bastante, para así compensar todas las veces que pierdes.
Como sabes, esta relación entre lo que ganas si ganas y lo que pierdes si pierdes cuando planteas una operación, es lo que llamamos la relación Beneficio/Riesgo (o ratio B/R, para los amigos).
B = | objetivo – entrada |
R = | entrada – stop loss |
B/R = | objetivo – entrada | / | entrada – stop loss |
En la práctica, si entras en el mercado a un cierto precio, el B/R es la distancia hasta tu objetivo, entre la distancia hasta tu stop loss. Y cuanto mayor sea mejor para ti, porque tienes mayor beneficio potencial a cambio de menor riesgo potencial.
El ratio B/R te lo da la operación, puesto que tanto el precio de entrada, como el objetivo, como el stop loss, son tres puntos que obtienes del gráfico, atendiendo a la lógica de tu operación. No los colocas donde quieres, sino donde tiene sentido. Esto hace que, para cada oportunidad, el ratio B/R te venga dado.
La cuenta mágica
La pregunta es ¿y el ratio B/R de esta operación me vale? Si es muy bajo, no me compensa operar, porque tenderé a ganar poco y perder mucho, y en global no ganaré.
Dicho con otras palabras ¿Cuál es el ratio B/R mínimo que tiene que tener una operación para que a mi me compense entrar?
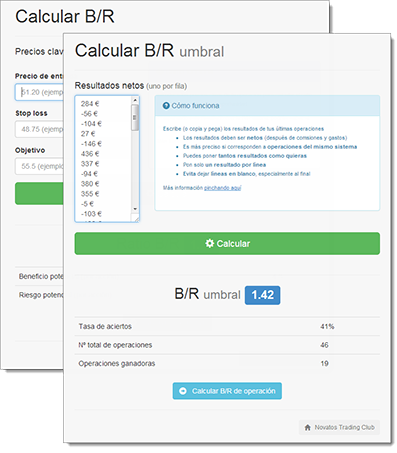
Esta es la cuenta mágica: El cálculo del B/R umbral
B/R umbral = 1 / g – 1
- Donde g es la tasa de aciertos en tanto por uno.
- La definición de acierto es aquella operación cuyo beneficio neto es positivo.
- Beneficio neto es el obtenido después de comisiones y otros gastos.
Veamos un ejemplo práctico
Supongamos que de mis últimas 30 operaciones, gané 13. Eso me da una tasa de aciertos del 43%.
g= 13/30 = 0.43
Con esto, yo sé que mi B/R umbral es de:
B/R umbral = 1 / 0.43 – 1 = 1.31
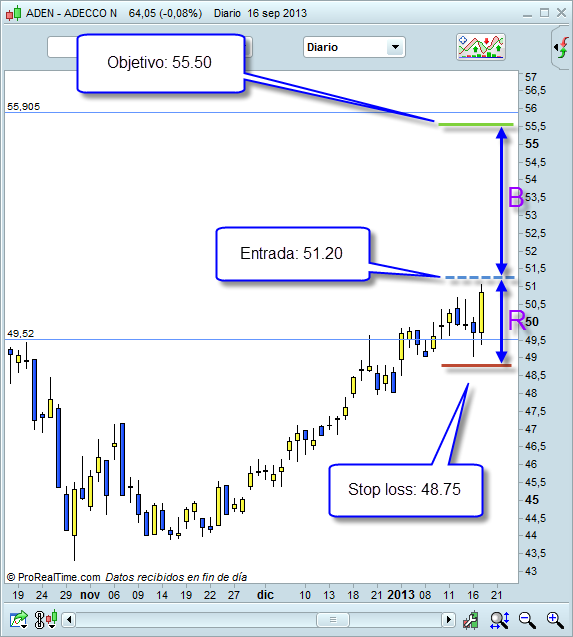
Y ahora yo me encuentro con esta oportunidad ¿Me compensa operar o no?
Con estos datos, calculamos el ratio B/R:
B = | 55.50 – 51.20 | = 4.30
R = | 51.20 – 48.75 | = 2.45
B/R = 1.76
Como esta oportunidad, que voy a operar según mi esquema de siempre y que cumple mis condiciones de siempre, tiene un B/R (1.76) superior a mi B/R umbral (1.31) puedo ejecutarla porque me compensa arriesgarme.
Es decir, aunque la pierda, sé que haciendo más como esta, en global acabaré ganando.
Ahora, un regalito para ti
Te ahorraré los trámites de que tengas que echar las cuentas a mano o de programártelas en un excel. Ya lo he hecho yo por ti:
He programado dos calculadoras: Una para que averigües tu B/R umbral a partir de tus últimos resultados y otra para que puedas calcular en cualquier momento el ratio B/R de una operación.
El recurso es gratuito, consíguelo pinchando en alguno de estos enlaces:
Calculadora de B/R de operación
Ahora me encantaría ver tus dudas y comentarios 🙂
Uxío Fraga (Trader y fundador)
Hola Uxío
Primero muchas gracias por toda la información y ayuda que nos das. No suelo poner ningún comentario porque estoy empezando, y realmente no tengo grandes dudas.
Pero te agradecería me enviaras las hojas de cálculo, porque aunque ya he compartido en tweeter, no se porqué pero no puedo verlas. Me salen unas pantallas con datos y boton calcular, pero no hace nada.
Muchísimas gracias
gustavo, no lo obtienes. Como dices, no puedes.
Lo que haces es suponer tu B/R umbral en 2 o 2.5 y operar una buena temporada así. Luego, con los datos en la mano, ya te puedes hacer una idea más precisa.
Un saludo y gracias por comentar
buenas noches, primero que nada lo felicito por esta gran guía, soy nuevo no se absolutamente nada pero estoy interesado en aprender, he leído y me ataca una duda, para el calculo B/R umbral colocas de ejemplo de 30 operaciones y sacas un valor, en el caso que soy novato y q no he hecho ninguna operación como obtengo ese resultado?, gracias
Aquí tienes: https://www.novatostradingclub.com/analisis-tecnico/como-identificar-soportes-y-resistencias/
Hola, enhorabuena uxío por este y otros temas que nos enseñas, gracias.
Como se calcula o donde viene dado el soporte o resistencia proxima?
Alguien me puede explicar esto, gracias
Enviadas a todos : )
Hola Uxio.
Acabo de intentar hacerlo por facebook pero hace años que no entro, podias enviarme las calculadoras por correo
Uxío , muchas gracias por tus enseñanzas.
Me podrías enviar las calculadoras para empezar con ellas cuanto antes?
Gracias.
Hola Uxio,soy otro novato en esto de la bolsa. Muy agradecido por toda la información que compartes con lo demás.
Podrías enviarme la calculadora B/R?
Gracias
Uxio, me han sido muy utiles tus análisis, trate de compartir en Face y no me sale. Podrías enviarme la calculadora.
Gracias
Hola Uxio,
Me parece interesa esta calculadora B/R, podrías enviarmela?. Gracias.
Uxío,
Yo soy otro agradecido por tu pasión por la enseñanza y por tus consejos, he tenido la suerte de ganar en mi primer movimiento pero ya he empezado aplicar tus consejos para no ser un perdedor.
Si me mandas las calculadoras empezare a no hacer nada si ellas no me dicen que merece la pena.
¡¡¡Menos mal que existen personas a las que les gusta enseñar¡¡¡¡ 🙂
Hola a todos!!!
Soy novato, fantastico tu trabajo Uxio.
Me envias las calculadoras?
Gracias, gracias y gracias.
Sí, así es.
En realidad, uno debe aspirar al B/R realista lo más alto que pueda y, como mínimo, no bajar de 2.
Después, a la hora de la verdad, uno tendrá un B/R umbral bastante menor y, en caso de encontrar oportunidades muy «claras», aún con un B/R bajo, siempre es conveniente saber dónde está el límite de lo admisible.
Personalmente, aunque en la teoría admito B/R de tan sólo 1.8 (y esta es mi referencia rápida para saber que nunca me acerco al B/R umbral), en la práctica hace mucho tiempo que no cojo nada por debajo de 2.3. Siempre hay oportunidades iguales o mejores con B/R superiores.
Gracias Uxío.
Entonces entiendo que he de usar umbral > 2, a no ser que la calculadora me indique que puedo usar un determinado umbral <= 2 (lo cual solo pasará si tengo un buen porcentaje de acierto).
Si es así, está clarísimo, profe.
Saludos.
Yo lo simplifico más y recomiendo ir siempre a por B/R > 2 como condición indispensable para aceptar una oportunidad.
Gracias Uxío,
Se calcule como se calcule el umbral, se necesita como dato el porcentaje de aciertos.
Pero hay dos casos complicados.
1.- Caso en que uno debuta con tu sistema. Aún no ha hecho ninguna operación. ¿Qué hacer? ¿Suponer que el porcentaje de aciertos será del 50% y calcular el umbral? ¿Ir con pies de plomo, comprando (en el caso largo) unos 3 ticks por encima de la zona de soporte, con objetivo unos 3 ticks por debajo se la resistencia, y stop loss por debajo de la zona de soporte?
2.- Caso en que uno ha hecho varias operaciones y todas perdiendo. Por ejemplo, empezar con una racha de 5 operaciones perdedores. ¿Qué hacer?
Yo supongo que hasta que aparezca una operación ganadora, mejor ir con pies de plomo, siendo muy selectivo. Y cuando uno aumente su porcentaje de aciertos, podrá operar calculando el umbral y no ser tan selectivo.
¿Cómo lo ves?
Saludos.
Rafa7, muchas gracias por la aportación, aunque la variación que propones complica demasiado las cosas en mi opinión.
Hola Uxío,
Una cosa muy personal es el riesgo de ruina (RoR = Risk-of-Ruin) que uno tolera. Había sugerido un 1%. Pero pienso que si un trader se siente cómodo arriesgando un 2% de capital, probablemente se sentirá cómodo con un riesgo de ruina del 2%. Este es un pensamiento por simetría.
La fórmula RoR = exp(- 2 * Kelly / fracción_riesgo), que es una buena aproximación cuando Kelly es próximo a cero, la podemos aplicar al 2% de riesgo que podríamos proponernos.
Despejando Kelly obtenemos esta otra fórmula:
Kelly = -0,5 * fracción_riesgo * Ln(RoR)
Y substituyendo RoR = 0,02, y fracción_riesgo = 0,02, tenemos:
Kelly = -0,5 * 0,02 *Ln(0,02) = 0,03912023005 = 0.04
Este es el Kelly que necesitamos conseguir para que arriesgando un 2% de capital en cada operación con un riesgo de ruina también del 2%.
Ahora bien, por definición, Kelly es esto:
Kelly = g – (1 -g) / B
Donde g es la fracción de acierto y B el umbral.
Despejando B tenemos:
B = (1 – g) / (g – Kelly)
Y sustituyendo Kelly por 0.04, tenemos:
B = (1 – g) / (g – 0,04)
La fórmula que propones es
B = 1 / g – 1, la cual sería equivalente a la que yo propongo sustituyendo Kelly por cero:
B = (1 – g) / (g – 0) = (1 – g) / g = 1 / g – 1
La fórmula B = 1 / g – 1 es para obtener una esperanza matemática positiva.
Pero la fórmula B = (1 – g) / (g – 0,04) es para obtener no solo una esperanza matemática positiva sino, además, un riesgo de ruina inferior al 2%. Te propongo que incorpores esta mejora en la calculadora. La cuestión es si un riesgo de ruina del 2% se considera demasiado conservador o poco conservador, o apropiado.
En el ejemplo, con g = 43% y aplicando la fórmula que propongo, tenemos:
B = (1 – 0,43) / (0,43 – 0,04) = 0,57 / 0,39 = 1,46
Dios te bendiga.
Muy buenas Uxío.
Antes que nada decir que me encanta tu blog, hace pocos días que llevo investigando y leyendome cada uno de tus posts por la curiosidad que siempre he tenido hacia la bolsa (algo que me ha parecido muy muy lejano y que ahora veo bastante más cerca y claro gracias a tu ayuda). Reconozco que aunque me encantaría, aún no dispongo ni de dinero ni valor cómo para entrar a jugar, pero la curiosidad cada día crece más y por fin encuentro una página capaz de explicarme el mercado bursátil como dios manda!
Si no es molestia me encantaría tener la calculadora que has hecho (aunque lo más probable es que me trabaje un EXCEL yo también por aquello de probar por mi cuenta).
De nuevo muchas gracias por tus explicaciones!
Enviada por email 🙂
Muchísimas gracias Uxío por tu gran aportación de conocimiento a todos los que somos novatos en este mundo!
Me podrías enviar la calculadora, no tengo prisa… Muchas gracias.
(Entonces no entiendo por qué sí sabes de dónde sale el stop loss)
Cógete el gráfico del ejemplo en ProRealTime y traza la horizontal en ese nivel (55.9) y míralo con perspectiva. Dime qué ves.
Mirándo el histórico ¿Qué es lo que suele pasar cuando el precio llega a 55.9?
Sinceramente, no tengo ni idea 😀
¿Esa línea qué es?
Un poco por debajo de la línea de 55.905, pero no sé por qué…
Mira la foto del ejemplo ¿Dónde pongo el objetivo?
Saludos a todos, y al autor enhorabuena por este fantástico blog!!
Mi duda es la siguiente: se dice en el post que, para calcular el ratio B/R, tenemos que tanto el objetivo como la entrada como el stop loss nos vendrán dados… yo entiendo que, de manera obvia, tendremos la entrada y el stop pero…y el objetivo de dónde sale?
Me parece muy buen sistema, te ayuda a disciplinarte.Hace tiempo que te sigo. tus explicaciones me parecen claras, aunque a veces sea dificil aplicarlas. Me podrías enviar la calculadora de B/R. Gracias. Ya formo parte del club
Me parece muy buen sistema, te ayuda a disciplinarte.Hace tiempo que te sigo. tus explicaciones me parecen claras, aunque a veces sea dificil aplicarlas. Me podrías enviar la calculadora de B/R. Gracias.
De todas formas no siempre llega a donde tu quieres. Recuerdo el año pasado, y el anterior, con una curva de beneficio/nº de operaciones estupenda, ganando muy bien, si miraba mis resultados eran, por ejemplo:
Pierdo 100€
Gano 120€
Gano 300€
Pierdo 100€
Gano: 100€
Pierdo: 100€
Gano: 400€
Pierdo: 100€
Pierdo: 100€
Pierdo: 100€
Gano: 110€
Gano: 340€
Relación B/P: Entre 40% y 60% siempre, no salía de ahí.
algo así y como ves gano muchas veces lo mismo que pierdo, por mucho que aspire a 3:1 al final muchas veces salta el stop en 1,2:1 o en 1:1 y mas en movimientos laterales. Lo que me resultaba curioso de esto es que parece que los movimientos de la bolsa, supongo que por el cuidador, prácticamente nunca me hacen ganar mas de 500€, por decir algo, me refiero a 5:1 o 5% para 1% de pérdida máxima, siempre al llegar a 4:1 o 5:1 se gira, además llevo 2 años y alucino con la frecuencia que veo esto. Creo que jamás he ganado mas de un 5:1, aunque las veces que lo hago te apañan el año claro, con pocas veces que hagas un 5:1 ese año sacas muy buen año. Cuando ganas un 5:1, lo que hace que mejore tu curva B/Nº op.
De acuerdo Rafa7, ya está corregida.
Sólo falta agregar que tanto B como R son ganancia promedio y pérdida promedio respectivamente.
La diferencia con Van K. Tharp es que él no usa la expectativa por operación entre las pérdidas promedio como lo hace Uxío, sino la expectativa por operación entre una pérdida máxima que escoges a través de tu operativa (puede ser lo máximo que estás dispuesto a perder por operación, 1-2% de tu capital), pero el concepto es el mismo.
En los cálculos y gráfica de f-óptima que nos proporcionó Uxío aparece como lo hace él.
Saludos.
Jejeje, Naby, he vuelto a equivocarme en una cosa, la primera expectativa, M, es expectativa por unidad de inversión, y la segunda expectativa, E, es expectativa por unidad de riesgo.
Estoy acostumbrado a participar en foros donde puedes corregir lo posteado. Por eso me precipito tanto y no tengo en cuenta que aquí no puedes modificar lo posteado.
El razonamiento queda así:
El razonamiento te lo vuelvo a escribir:
La expectativa por unidad de inversión es:
M = g * B – (1 – g) * R
Donde
M expectativa por unidad de riesgo
g probabilidad de acierto
B cuanto ganas cuando ganas
R cuanto pierdes cuando pierdes, en valor absoluto
La expectativa por unidad de riesgo es:
E = M / R = (g * B – (1 – g) * R) / R = g * B / R – (1 – g) = g * B / R – 1 + g = g * (B / R + 1) – 1
Donde E es la expectativa por unidad de riesgo.
Por tanto,
E = g * (B / R + 1) – 1
Saludos.
Hola noby,
Cometí un error de signo, la esperanza matemática no es M = g * B + (1 – g) * R sino M = g – (1 – g) * R, ya que estoy suponiendo R en valor absoluto (aunque no lo especifiqué), o sea positivo. Y voy a corregir los términos, ya que sospecho que esperanza y expectativa sean sinónimos.
Gracias por estar atento y señalarme el error.
El razonamiento te lo vuelvo a escribir:
La expectativa por unidad de riesgo es:
M = g * B – (1 – g) * R
Donde
M expectativa por unidad de riesgo
g probabilidad de acierto
B cuanto ganas cuando ganas
R cuanto pierdes cuando pierdes, en valor absoluto
La expectativa por unidad de riesgo es:
E = M / R = (g * B – (1 – g) * R) / R = g * B / R – (1 – g) = g * B / R – 1 + g = g * (B / R + 1) – 1
Donde E es la expectativa por unidad de riesgo.
Por tanto,
E = g * (B / R + 1) – 1
Saludos.
Gracias por tu interes Rafa7,
Porqué le cambiaste el signo al segundo término de M, para dedudir E?.
Voy a retomar esto nuevamente y, posteriormente te envío la manera en que lo calcula Van K. Tharp, la cual difiere aprox. el 90% en los resultados calculados con la E que enviaste, y que es la misma que maneja Uxío.
Noby,
Quiero aclarar los términos que he usado de esperanza matemática y expectativa. No estoy seguro de cuales son las convenciones. Porque esos términos mirándolos en un diccionario parecen sinónimos. Y veo que hay autores de artículos, o libros, de trading que usan la palabra expectativa para referirse a la expectativa por unidad de inversión o a la expectativa por unidad de riesgo.
La fórmula que mencionas se refiere a la expectativa por unidad de riesgo. Y lo que yo he llamado esperanza matemática tal vez se la pueda llamar expectativa por unidad de inversión.
Saludos.
Noby,
Te escribo el razonamiento completo, ya corregido:
La esperanza matemática, es la ganancia por cada euro invertido:
M = g * B + (1 – g) * R
Donde
M esperanza matemática
g probabilidad de acierto
B cuanto ganas cuando ganas
R cuanto pierdes cuando pierdes
La expectativa es la ganancia por cada euro arriesgado, o sea:
E = M / R = (g * B – (1 – g) * R) / R = g * B / R – (1 – g) = g * B / R – 1 + g = g * (B / R + 1) – 1
Donde E es la expectativa.
Por tanto,
E = g * (B / R + 1) – 1
Saludos.
Noby,
Perdón, una pequeña errata.
Esto está mal: M = g * B + (1 – g) / R
Lo correcto es M = g * B + (1 – g) * R.
Qué siguiendo el razonamiento de mi post anterior, llegaremos a la conclusión de que:
E = g * (B / R + 1) – 1
Ya que E = M / R = (g * B – (1 – g) * R) / R = g * B / R – (1 – g) = g * B / R – 1 + g = g * (B / R + 1) – 1
Saludos.
Hola Noby,
Preguntas por de donde sale la fórmula de la Expectativa: Expectativa = g * (B / R + 1) -1
La esperanza matemática, es la ganancia por cada euro invertido:
M = g * B + (1 – g) / R
Donde
M esperanza matemática
g probabilidad de acierto
B cuanto ganas cuando ganas
R cuanto pierdes cuando pierdes
La expectativa es la ganancia por cada euro arriesgado, o sea:
E = M / R = (g * B – (1 – g) * R) / R = g * B / R – (1 – g) = g * B / R – 1 + g = g * (B / R + 1) – 1
Por tanto,
E = g * (B / R + 1) – 1
Saludos.
Servido : )